|
在此僅簡單介紹假設檢定之相關名詞、公式以及應用,若欲進一步閱讀請參考黃文璋(2003).
數理統計第八章,華泰文化事業股份有限公司。
假設檢定名詞介紹
|
名稱 |
說明 |
|
假設檢定
之流程 |
- 猜想(假定)
 收集資料 收集資料 檢定 檢定 作決策(接受或拒絕猜想)。 作決策(接受或拒絕猜想)。
|
|
統計假設
(hypothesis) |
-
一個關於母體分佈之斷言或猜想。
-
一個關於母體之敘述(statement)。
-
統計假設分為兩部分:
 虛無假設(null hypothesis),以符號 虛無假設(null hypothesis),以符號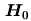 表之。 表之。
 對立假設(alternative
hypothesis)以符號 對立假設(alternative
hypothesis)以符號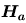 (或 (或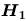 , ,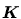 )表之。 )表之。
-
統計假設又可分為:簡單假設和複合假設。
 簡單假設(simple
hypothesis): 簡單假設(simple
hypothesis):
例如: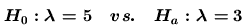 。 。
 複合假設(composite
hypothesis): 複合假設(composite
hypothesis):
例如: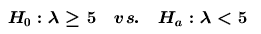 。 。
|
|
統計推論
(statistical
inference) |
|
|
假設檢定
(testing
hypothesis) |
- 基於母體之一組隨機樣本
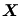 ,以決定兩個假設( ,以決定兩個假設(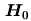 , ,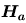 )中何者該拒絕。 )中何者該拒絕。
|
|
接受域
(acceptance
region)
拒絕域
(rejection
region) |
-
接受域:使虛無假設被接受之集合。
-
拒絕域:使虛無假設被拒絕之集合。
|
|
檢定
(test)
|
-
決定一檢定,即表決定拒絕域及接受域。
-
對一檢定,以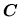 為拒絕域,即拒絕 為拒絕域,即拒絕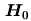 ,若且為若 ,若且為若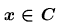 。 。
-
統計檢定之可能結果:
|
|
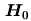 為真 為真
|
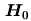 不真 不真
|
|
接受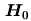 |
正確 |
型II錯誤(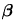 ) ) |
|
拒絕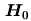 |
型I錯誤(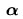 ) ) |
正確 |
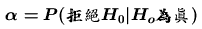

|
|
顯著水準
(significance
level) |
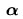 稱為顯著水準,又稱為檢定大小。 稱為顯著水準,又稱為檢定大小。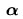 之值常取成0.1,0.05或0.01等。 之值常取成0.1,0.05或0.01等。
|
|
檢定統計量
(test
statistic) |
|
|
p-值
(p-value) |
|
T-檢定
(Student's
T distribution)
|
名稱 |
說明 |
|
單樣本T-檢定
(one
sample T-test) |
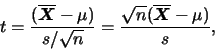
有自由度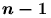 的T-分佈。( 的T-分佈。(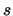 表樣本標準差)。 表樣本標準差)。
|
|
二樣本T-檢定
(two-
sample
T-test)
|
假設有兩組獨立的隨機樣本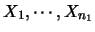 及 及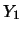 , ,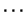 , ,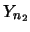 ,分別有 ,分別有
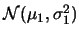 及 及
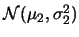 。 令 。 令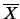 , , 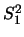 及 及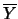 , ,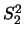 分別表第一組及第二組樣本之樣本平均及樣本變異數。則 分別表第一組及第二組樣本之樣本平均及樣本變異數。則
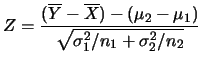
有
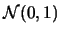 分佈。又 分佈。又
則
若
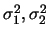 未知且不相等, 則 未知且不相等, 則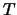 並非統計量。
但若 並非統計量。
但若
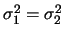 ,則 ,則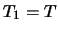 , 其中 , 其中
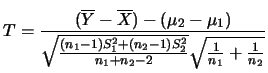
為一有
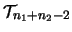 分佈之統計量。 分佈之統計量。
|
注意:請先
load package
"ctest"。(若為新版
R1.9.0版,則此 package改
為"stats"。)
-
T-檢定:t.test(x,
y=NULL, alternative=c("two.sided", "less",
"greater"), mu=0, paired=FALSE, var.equal=FALSE,
conf.level=0.95)。
參數說明:
-
x:欲做檢定的資料,必須是數值向量物件;
-
y:欲做兩個樣本檢定的另一筆資料,必須是數值向量物件,預設為
"NULL" 表示只有單一樣本的檢定;
-
alternative:為檢定中的對立假設,必須為
"two.sided",
"less", "greater"其中一項,預設為
"two.sided";
-
mu:若為單一樣本則表示"mean"的值,若為兩個獨立樣本則表示兩個樣本"mean"的差距;
-
paired:是否為成對樣本,預設為"FALSE";
-
var.equal:兩個樣本的"variance"是否相等,預設為"FALSE";
-
conf.level:信賴區間的信心水準,預設為"0.95"。
資料說明:
利用已知分佈(常態分佈)生成隨機亂數並進行檢定分析。
生成三組常態分佈的隨機亂數資料,分別為
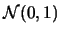 , ,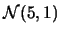 , ,
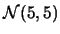 ,每組資料各有10筆數據。 資料內容如表
1。 ,每組資料各有10筆數據。 資料內容如表
1。
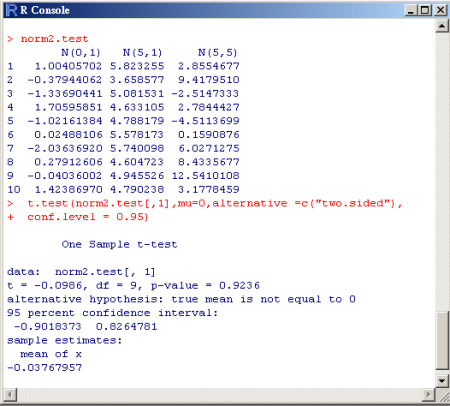
 單樣本T檢定之例: 單樣本T檢定之例:
由單樣本之T檢定的結果可知檢定統計量
t 為 -0.0986,且其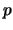 值為0.9236,
此 值為0.9236,
此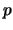 值大於所設定的顯著水準 值大於所設定的顯著水準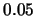 。 故由分析結果知此筆數據不拒絕虛無假設 。 故由分析結果知此筆數據不拒絕虛無假設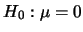 。 在分析結果中,
也列出了95%信賴區間及樣本平均。 。 在分析結果中,
也列出了95%信賴區間及樣本平均。
範例程式碼:
>norm2.test<-data.frame(rnorm(10,mean=0,sd=1),
+ rnorm(10,mean=5,sd=1),rnorm(10,mean=5,sd=5))
>
t.test(norm2.test[,1],mu=0,alternative =c("two.sided"),
+ conf.level = 0.95)
|
 二樣本T檢定之例:(假設變異數相等) 二樣本T檢定之例:(假設變異數相等)
利用表
1的
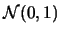 及 及
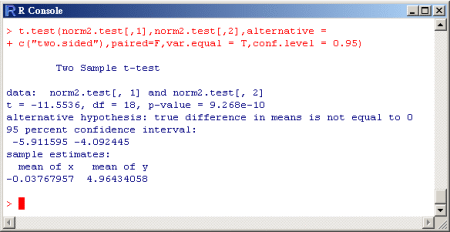
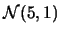 之數據來進行二樣本之T檢定分析。指令與單樣本之T檢定為同一指令,即“t.test”。若一開始並不知道此二筆數據,
是由 之數據來進行二樣本之T檢定分析。指令與單樣本之T檢定為同一指令,即“t.test”。若一開始並不知道此二筆數據,
是由
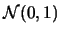 及 及
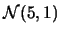 分佈所產生的,且假設變異數 分佈所產生的,且假設變異數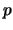 是相等的,利用T檢定來作分析, 可得其 是相等的,利用T檢定來作分析, 可得其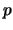 值為9.268e-10,此值小於所設定的顯著水準 值為9.268e-10,此值小於所設定的顯著水準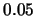 。
故由分析結果知此數據拒絕虛無假設 。
故由分析結果知此數據拒絕虛無假設
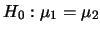 。同樣的,
在分析結果中,
也列出了95%信賴區間及二組資料的樣本平均。 。同樣的,
在分析結果中,
也列出了95%信賴區間及二組資料的樣本平均。
範例程式碼:
>
t.test(norm2.test[,1],norm2.test[,2],alternative =
+ c("two.sided"),paired=F,var.equal = T,conf.
+ level = 0.95)
|
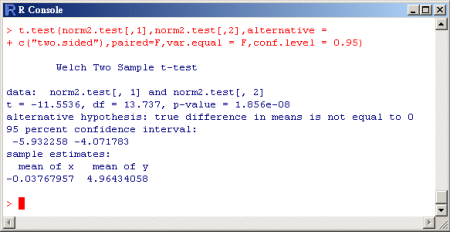
 二樣本T檢定之例:(假設變異數不相等) 二樣本T檢定之例:(假設變異數不相等)
若假設變異數是不相等的,可得其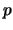 值為 1.856e-8,
此 值為 1.856e-8,
此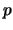 值小於所設定的顯著水準 值小於所設定的顯著水準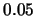 。
故由分析結果知此數據同樣拒絕虛無假設 。
故由分析結果知此數據同樣拒絕虛無假設
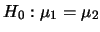 。同時也在分析結果中,列出了95%信賴區間及二組資料的樣本平均。 。同時也在分析結果中,列出了95%信賴區間及二組資料的樣本平均。
範例程式碼:
>
t.test(norm2.test[,1],norm2.test[,2],alternative =
+ c("two.sided"),paired=F,var.equal = F,
+ conf.level = 0.95)
|
F-檢定
(F-
test)
注意:請先
load package
"ctest"。(若為新版
R1.9.0版,則此 package改
為"stats"。)
-
F-檢定:var.test(x,
y, ratio=1, alternative=c("two.sided", "less",
"greater"), conf.level=0.95)。
參數說明:
-
x,
y:分別為兩個樣本的資料,必須是數值向量物件;
-
ratio:樣本"x"的變異數與樣本"y"的變異數的比值,預設為"1";
-
alternative:為檢定中的對立假設,必須為
"two.sided",
"less", "greater"其中一項,預設為
"two.sided";
-
conf.level:信賴區間的信心水準,預設為"0.95"。
資料說明:
利用表
1的
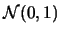 及 及
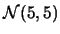 數據來進行變異數的檢定分析。指令為“
var.test”。若一開始並不知道此二筆數據,是由 數據來進行變異數的檢定分析。指令為“
var.test”。若一開始並不知道此二筆數據,是由
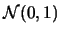 及 及
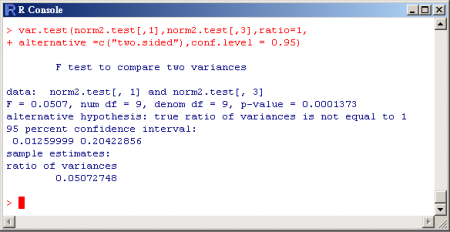
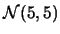 分佈所產生的,利用變異數檢定分析可得其 分佈所產生的,利用變異數檢定分析可得其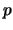 值為0.0001373,此 值為0.0001373,此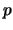 值小於所設定的顯著水準 值小於所設定的顯著水準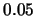 。
由分析結果知此數據拒絕虛無假設 。
由分析結果知此數據拒絕虛無假設
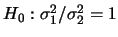 。同樣的,在分析結果中,亦列出了95%信賴區間及二組資料之樣本變異數的比例值。 。同樣的,在分析結果中,亦列出了95%信賴區間及二組資料之樣本變異數的比例值。
範例程式碼:
> var.test(norm2.test[,1],norm2.test[,3],ratio=1,
+ alternative =c("two.sided"),conf.level = 0.95)
|
卡方檢定
(chi-square
test)
|
名稱 |
說明 |
|
卡方檢定
(chi-sqaure
test) |
-
卡方檢定又稱為皮爾生之卡方適合度檢定(Pearson's
chi-square goodness-of-fit test),是最常用的適合度檢定法之一。
-
"fit"一詞,就是指機率模型是否合適。
-
對一隨機現象,由收集到的數據,想檢定某一模型對此組數據是否合適。
-
想區別數據的偏差是由於機運所產生,或真的是因模型不夠精確,這種過程變統稱為適合度檢定。
-
皮爾生卡方(Pearson
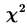 )統計量為 )統計量為
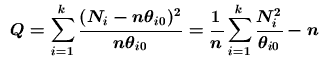 。 。
顯然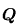 是在測量在 是在測量在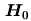 之下,觀測頻率 之下,觀測頻率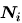 與期望頻率 與期望頻率
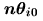 之差異情況。 之差異情況。
|
注意:請先
load package
"ctest"。(若為新版
R1.9.0版,則此 package改
為"stats"。)
-
卡方檢定:chisq.test(x, y = NULL,
correct = TRUE,
p = rep(1/length(x), length(x)),simulate.p.value = FALSE, B = 2000)。
參數說明:
-
x:為向量或矩陣物件。
-
y:
向量物件。若"x"唯一矩陣物件則省略"y";
-
correct:是否作連續性修正,預設為
"TRUE";
-
p:與"x"有相同長度之向量的機率;
-
simulate.p.value:是否利用Monte Carlo simulation計算p-值;
-
B:利用Monte Carlo simulation所須之筆數。
資料說明:
以孟德爾著名的關於豌豆生長的實驗為例。他將有圓黃(round
yellow)種子的與有縐綠(wrinkled green)種子的豌豆雜交。依其理論,會生長出圓黃、圓綠、縐黃及縐綠種子的後代之比率,應分別為9/16,
3/16, 3/16及1/16。經由一組有556個樣本的實驗,我們列出觀測頻率及期望頻率於表
2。
表 2 豌豆雜交後生長的觀測頻率及期望頻率
| |
圓黃 |
圓綠 |
縐黃 |
縐綠 |
| 觀測頻率 |
315 |
108 |
101 |
32 |
| 期望頻率 |
312.75 |
104.25 |
104.25 |
34.75 |
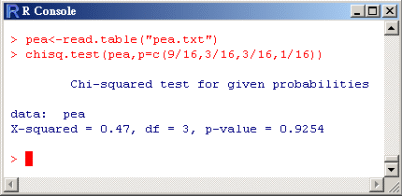
由表 2的資料,利用R的卡方檢定之指令“chisq.test”,所得結果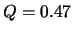 , , 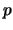 值為0.9254。因此無法拒絕虛無假設 值為0.9254。因此無法拒絕虛無假設
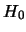 :孟德爾的理論為正確。 :孟德爾的理論為正確。
範例程式碼:
> pea<-read.table("pea.txt")
> chisq.test(pea,p=c(9/16,3/16,3/16,1/16))
|
最大概似估計法
(method of maximum
likelihood)
最大概似估計的理論架構及性質, 請參考請參考黃文璋(2003)。華泰文化事業股份有限公司。
|
名稱 |
說明 |
|
最大概似估計法
(method of maximum
likelihood)
|
|
注意:請先
load package
"MASS"。
參數說明:
資料說明:
利用R生成10筆
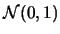 的數據,如表 3。
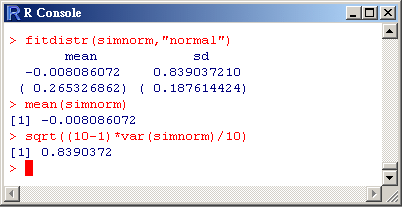
由R的指令計算後可得此筆資料的 的數據,如表 3。
由R的指令計算後可得此筆資料的
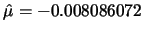 及 及
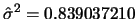 ,由公式推導的結果 ,由公式推導的結果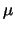 及 及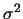 之最大概似估計值分別為 之最大概似估計值分別為
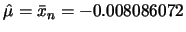 及 及
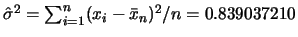 。 。
表 3 由
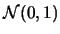 生成之10筆數據 生成之10筆數據
|
1
|
-1.25494872994457
|
2
|
0.580494591832429
|
| 3 |
-0.203463056389231 |
4 |
0.0507923242732363 |
| 5 |
-0.400148582512666 |
6 |
-0.133561998301612 |
| 7 |
-1.48978604201467 |
8 |
0.883319416939335 |
| 9 |
1.19584395609907 |
10 |
0.690597401520781 |
範例程式碼:
>
simnorm<- rnorm(10,mean=0,sd=1)
> fitdistr(simnorm,"normal")
>
mean(simnorm)  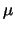 之最大概似估計值 之最大概似估計值
>
sqrt((10-1)*var(simnorm)/10) 
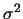 之最大概似估計值 之最大概似估計值
|
同樣地,利用R生成10筆指數分佈參數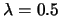 的數據, 如表 4。
透過R的計算可得 的數據, 如表 4。
透過R的計算可得
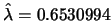 ,由公式推導的結果 ,由公式推導的結果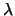 之最大概似估計值為 之最大概似估計值為
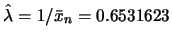 。 。
表 4 由參數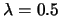 的指數分佈生成之10筆數據 的指數分佈生成之10筆數據
| 1 |
6.18360018696556 |
2 |
0.0952219185649138 |
| 3 |
0.92688906379044 |
4 |
0.783767773644048 |
| 5 |
0.849087740046285 |
6 |
0.37164671998471 |
| 7 |
2.23702448970618 |
8 |
0.509015057058229 |
| 9 |
0.381319892592728 |
10 |
2.97255648867447 |
範例程式碼:
>
simnorm<- rnorm(10,mean=0,sd=1)
>
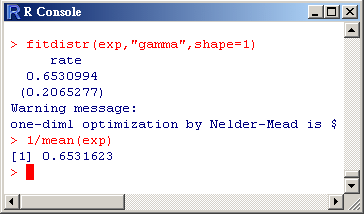
fitdistr(exp,"gamma",shape=1)
> 1/mean(exp)
  之最大概似估計值 之最大概似估計值
|
 從求常態分佈及指數分佈參數的最大概似估計值的結果中,可看出此指令為數值計算的結果會與實際利用公式推導出的估計值有些微誤差。
在常態分佈的例子中, 不論公式計算或透過R來求最大概似估計值皆可得到同樣的結果,但是在指數分佈的例子中,兩個估計值有些微的誤差,兩者的差為
0.000629。當樣本數夠多時此誤差值會越小。
從求常態分佈及指數分佈參數的最大概似估計值的結果中,可看出此指令為數值計算的結果會與實際利用公式推導出的估計值有些微誤差。
在常態分佈的例子中, 不論公式計算或透過R來求最大概似估計值皆可得到同樣的結果,但是在指數分佈的例子中,兩個估計值有些微的誤差,兩者的差為
0.000629。當樣本數夠多時此誤差值會越小。
區間估計
(interval
estimation)
|
名稱 |
說明 |
|
區間估計
(interval
estimation)
|
|
注意:請先
load package
"ctest"。(若為新版
R1.9.0版,則此 package改
為"stats"。)
參數說明:
同樣的方式也可只列出“t.test”檢定結果的單一個值, 只須將“
conf.int”改成所要求之值的指令即可, 對應的指令參考表
5
表 5 有關`` t.test''的一些細部指令
| 指令 |
對應指令的意義 |
| statistic |
檢定統計量的值 |
| parameter |
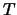 檢定的自由度 檢定的自由度 |
| p.value |
檢定的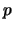 值 值 |
| conf.int |
信賴區間 |
| estimate |
參數的估計值 |
| null.value |
虛無假設的檢定內容, 檢定平均值或二平均值的差 |
| alternative |
虛無假設採用單邊或雙邊檢定 |
| method |
檢定方法,
單樣本檢定或雙樣本檢定 |
| data.name |
檢定的資料名稱 |
資料說明:
以表
3的數據為例,並假設此筆數據的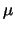 及 及
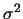 皆未知。 皆未知。
範例程式碼:
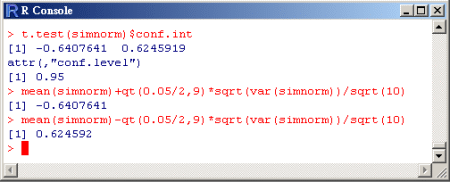
>
t.test(simnorm)$conf.int
> mean(simnorm)+qt(0.05/2,9)*sqrt(var(simnorm))/sqrt(10)
 由公式直接求得上信賴界 由公式直接求得上信賴界
> mean(simnorm)-qt(0.05/2,9)*sqrt(var(simnorm))/sqrt(10)
 由公式直接求得下信賴界 由公式直接求得下信賴界
|
|
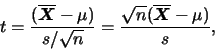
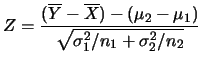
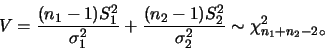
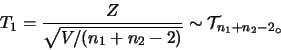
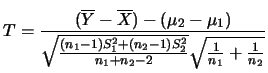



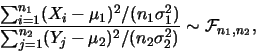
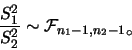




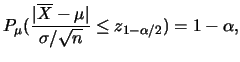
![$\displaystyle \left[\overline{X}-z_{1-\alpha/2}\frac {\sigma}{\sqrt{n}},
\overline{X}+z_{1-\alpha/2}\frac {\sigma}{\sqrt{n}}\right]$](estimate/img32.gif)
![$\displaystyle \left[\overline{X}-t_{1-\alpha/2,n-1}\frac {S}{\sqrt{n}},
\overline{X}+t_{1-\alpha/2,n-1}\frac {S}{\sqrt{n}}\right]$](estimate/img34.gif) 為
為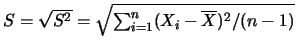 。
。