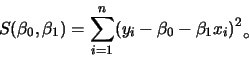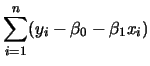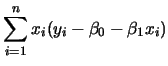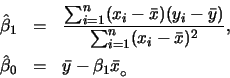|
簡單線性迴歸
-
配適最小平方法:lsfit(x,
y, intercept=TRUE, tolerance=1e-07, yname=NULL)
-
配適線性模型:lm(formula,
data, subset, method = "qr")
-
資料摘要整理:summary(object)
參數說明:
資料說明:(來源:統計軟體R之內建資料庫) 在此我們以老忠實噴泉的數據為例。此筆數據來自美國懷俄明(Wyoming)洲之黃石公園(Yellowstone
National Park)的老忠實噴泉(Old
Faithful geyser )。共記載了兩筆數據,一為兩次噴發的時間間隔,一為每次噴發維持的時間。其散佈圖如下: 
所配適的線性迴歸模型為
範例程式碼:
>
data(faithful)
> fit.faithful<-lm(eruptions~.,faithful)
> summary(fit.faithful)

|
我們先給出此例之變異數分析表。(關於變異數分析,我們之後會有詳細之介紹)。

由變異數分析表中的 統計量可用來檢定斜率是否為0,
即檢定 統計量可用來檢定斜率是否為0,
即檢定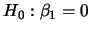 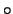 若要拒絕 若要拒絕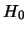 ,
則 ,
則
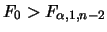  由資料顯示老忠實噴泉數據的 由資料顯示老忠實噴泉數據的
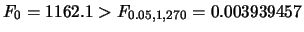 , 故拒絕 , 故拒絕 的假設。 的假設。
範例程式碼:
> aov.faithful<-aov(lm(eruptions~.,faithful))
> summary(aov.faithful)
|
另外,我們給出老忠實噴泉的殘差與配適值的散佈圖。

範例程式碼:
>
plot(fitted(fit.faithful),residuals(fit.faithful),pch=20,
+ xlab="fitted value",ylab="residuals")
|
單因子變異數分析
|
名稱 |
說明 |
|
變異數分析
(analysis
of variance, 或簡稱ANOVA)
|

|
|
單因子變異數分析
(one-way ANOVA)
|
其中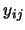 為第 為第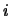 組資料中第 組資料中第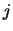 個觀測值, 個觀測值, 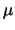 為 為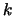 組的共同參數, 組的共同參數,
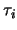 為影響第 為影響第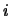 組結果的一個參數, 組結果的一個參數,
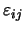 為一誤差項並且
滿足 為一誤差項並且
滿足
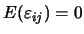 及 及
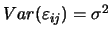 , ,
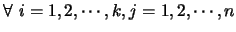 。 。
其中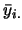 代表第 代表第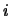 組中 組中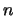 個觀測值的平均,
即 個觀測值的平均,
即
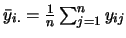 。 。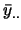 表示整體平均,
即
表示整體平均,
即
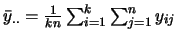 。 。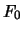 為檢定統計量,
且在 為檢定統計量,
且在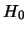 的假設下, 的假設下, 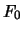 服從 服從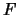 分佈, 自由度分別為 分佈, 自由度分別為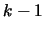 , ,
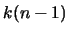 。故若 。故若
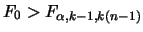 則拒絕 則拒絕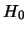 的假設,
反之則接受 的假設,
反之則接受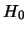 。 。
|
參數說明:
-
is.factor:檢查資料x是否為因子型態。
-
formula:配式模型的符號描述。
-
data:配式模型符號的描述。
資料說明:
Montgomery(2001)曾研究過關於男性襯衫織布的化學合成物纖維抗拉強度的實驗。
此強度是受由纖維中棉花的百分比所影響。資料內容如表 3。
表 3 纖維抗拉強度數據資料
| 棉花百分比 |
抗拉強度 |
| 15 |
7 |
7 |
15 |
11 |
19 |
| 20 |
12 |
17 |
12 |
18 |
18 |
| 25 |
14 |
18 |
18 |
19 |
19 |
| 30 |
19 |
25 |
22 |
19 |
23 |
| 35 |
7 |
10 |
11 |
15 |
11 |
範例程式碼:
> redanova<-read.table("anova.csv",sep=",",header=T)
> boxplot(Strength~Cotton,data=redanova,col=c(gray(0.8)),
+ xlab="percentage of Cotton",ylab="Tensile Strength",pch=20)

> if (!is.factor(redanova$Cotton))
+ redanova$Cotton<-factor(redanova$Cotton)
> a<-aov(Strength~Cotton, data=redanova)
> summary(a)

|
|