中央極限定理（Central Limit Theorem）


 
 

1.源由     2.方法     3.特性及應用     4.範例     5.操作
  1. 源由

    2. 中央極限定理 (Central Limit Theorem) 是機率理論及統計學中最重要且常用的結果之一。對許多初學者而言，卻是一個不容易瞭解的抽象概念。為了讓初學者比較容易瞭解及掌握中央極限定理的基本概念，這裡將藉由網路互動式模擬程式，來讓初學者從互動的實驗中理解中央極限定理的基本概念。
     
     
  2. 方法

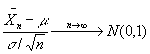    3. 中央極限定理 (Casella and Berger, 1990, p.216) 有時也稱為常態收斂定理，主要是指從平均數為 ，標準差為 的母體中，隨機地抽取大小為  的獨立樣本 。當樣本數  很大時，其樣本平均  減掉平均數  再除以標準差 ，將會趨近平均數為0，標準差為1 的常態分佈(normal distribution)。或者是說當樣本數  很大時，樣本和  減掉平均數  再除以標準差  ，將會趨近平均數為0，標準差為1 的常態分佈，即

    ，或 ，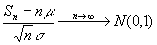

    所以  的圖形看起來將會很像常態分佈的鐘形。

    在此 Applet 中，將以擲  顆  面骰子的點數和  來模擬中央極限定理的趨近。在一般的情況下， 可以看做離散的均勻分佈，其機率密度為 ，期望值為 ，變異數為 ，所以  的期望值為 ，變異數為，因此當  夠大時，，即  將會趨近 。
     
     

  3. 特性及應用

    4. 在這 Applet 中，藉由模擬擲骰子所得到的點數和  會趨近常態分佈，來闡述中央極限定理的基本概念。

    對一般的母體而言，當樣本數  夠大時， 會趨近 。因此對  畫直方圖所得到的結果會隨著 的加大而越趨近此常態分佈的鐘形。

    在此 Applet 中將會把  所會趨近的常態分佈的分佈線給畫出來，用來跟所畫出來的常態直方圖作比較。

    由過去的實驗及文獻可以知道，只要投擲的骰子數大於等於30個，所得的圖形將與常態分佈非常的相近。而這個程式所做的模擬也的確與這個結論相吻合。
     
     

  4. 範例

    5. 由程式執行的結果可以看出，當實驗所投擲的六面骰子個數  為1時，如(圖九) 其實驗次數為 10000次，根據點數和  所畫出來的直方圖看起來不像鐘形，而是像均勻分佈的圖形，這是因為  本來就是離散的均勻分佈。

    當一次實驗所投擲的骰子數  為2時，如(圖十) 其實驗次數為 10000次，所得到的直方圖有一點像鐘形。

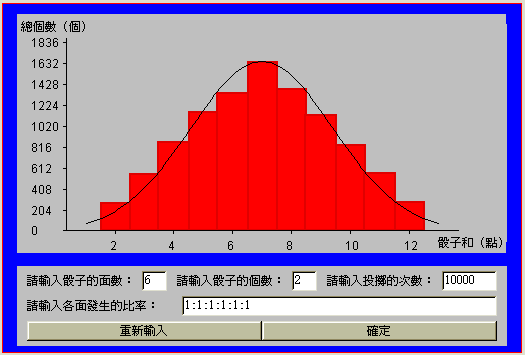
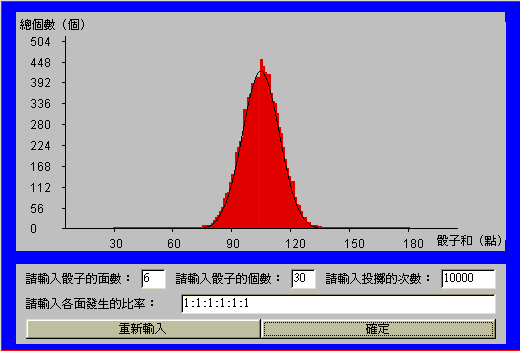
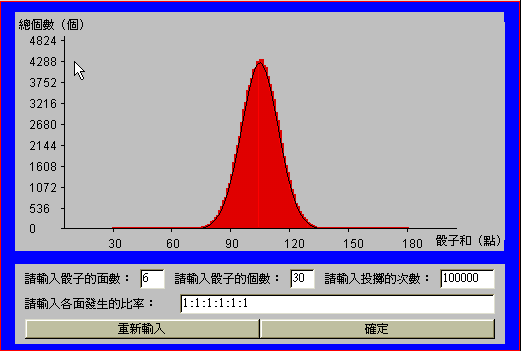
    當  為30 時，如 (圖十一）及 (圖十二) 其實驗次數各為10000及100000次，由所得到的圖形可以發現，直方圖越來越像鐘形且與常態分佈機率密度函數圖越來越吻合。

    　

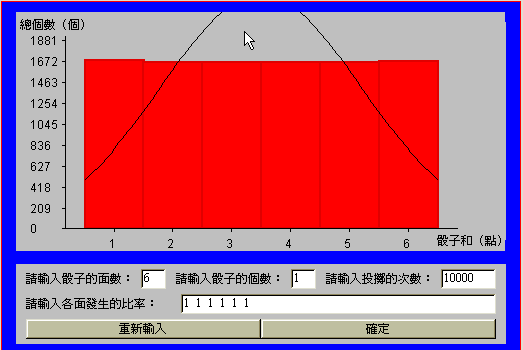
    (圖九) 中央極限 (圖十) 中央極限

    　 

    (圖十一) 中央極限 (圖十二) 中央極限

  5. 操作

    6. 使用者在使用這個程式時，必需先輸入一次實驗所欲投擲的骰子面數  (預設為6面)、每面發生的機率比 (預設為公平骰子1:1:1:1:1:1)、投擲的骰子個數  (預設30個)，以及實驗次數  (預設10000次)。

    在輸入完成後按確定，將可以看到紅色的  直方圖及黑色的  常態分佈機率密度函數曲線圖，然後藉由直方圖與曲線圖的比較可以知道模擬出來的結果與常態分佈的吻合程度。